いまさらながら高等学校情報科「情報Ⅰ」教員研修用教材の第3章のJavascript版を見ました。クイックソートについて、python版の方ではバグが報告されて、正誤表でクイックソートのプログラムの修正がされています。Javascript版は前の誤りがあったpython版プログラムを元にしているのか同様のバグがあるようなプログラムでした。プログラム自体は正誤表のクイックソートを参考にすれば、しっかり動くクイックソートが実装出来ます。
この記事では誤りがあったクイックソートについてのバグ修正について考えてみたいと思います。バグの原因の考察ですが、その考察にバグがあったらごめんなさい><
まず、誤りがあるクイックソートは以下のようになっています。

テキストとしてクイックソート部分だけを抽出すると以下のようになります。画像のソースコードとはインデントを少し変えています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
function quicksort(a, start, end){ m = parseInt((start+end)/2); i = start; j = end; while(i<j){ while(a[i] < a[m]){ i = i+1; } while(a[j] > a[m]){ j = j-1; } if(i>=j){ break; } temp = a[i]; a[i] = a[j]; a[j] = temp; if(i==m){ m = j; } else if(j==m){ m = i; } i = i+1; j = j-1; } if(start < i-1){ quicksort(a, start, m-1); } if(end > j+1){ quicksort(a, m+1, end); } } |
このクイックソートを用いて、例えば、
|
1 |
[3, 4, 5, 6, 7, 8, 9, 2, 1] |
のような配列をソートすると
|
1 |
1,2,3,4,5,6,8,9,7 |
のような出力になります。
何が原因か
このクイックソートは下の図のように両端からピボットより小さい値と大きい値を分けていくプログラムになっています。
このときピボットと同じ値はどちらの方にも入る可能性があるので、正確には組分け済みの配列にはそれぞれ等号を入れたほうがいいかもしれませんが図を作り直すのが面倒なのでこのまま説明に使います。
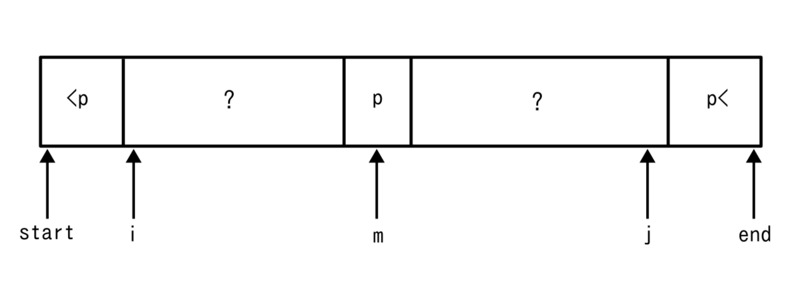
このとき、ループを正しく行うための制約としてプログラムには記述がありませんが、暗黙的にi<=mかつm<=jというものがあります。これは不変の表明(assertion)といってもいいものでしょう。不変の表明については「珠玉のプログラミング 本質を見抜いたアルゴリズムとデータ構造(2014,丸善出版)」を参照してください。もっと記述するなら、startからiまでの範囲の配列の要素の値はa[m]以下であるや、反対側のendからjまでの範囲の配列の要素の値はa[m]以上であるといってもいいかもしれません。
さて、バグが起こる該当部分はスワップ処理の
|
1 2 3 4 5 6 7 8 9 10 |
temp = a[i]; a[i] = a[j]; a[j] = temp; if(i==m){ m = j; } else if(j==m){ m = i; } i = i+1; j = j-1; |
部分になります。要素のスワップ処理は特に問題がありません。問題が出てくるのはピボットをスワップするときの処理になります。ピボットがスワップする場合は以下のように端からピボットまでの片側がすべて組分けが終わっている場合になります。
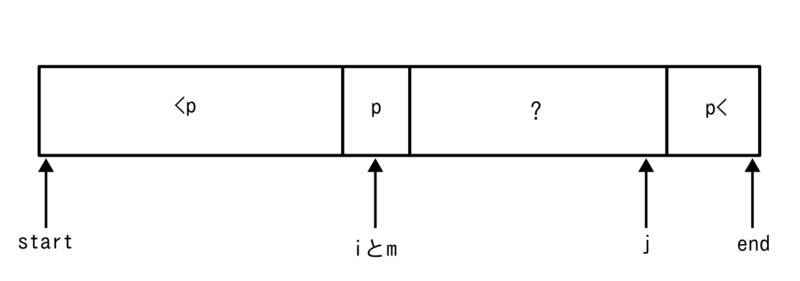
この状況でピボットのスワップ処理を行うと
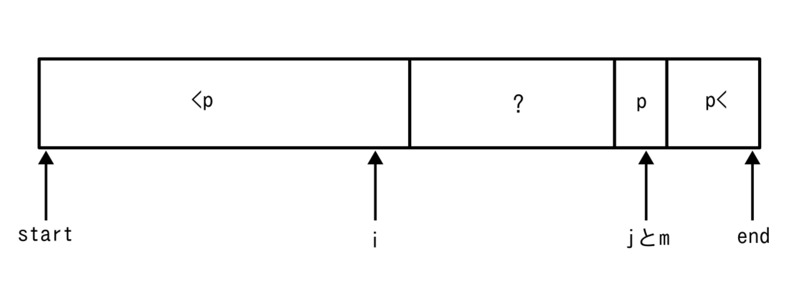
のようになります。この後にiとjを動かすと
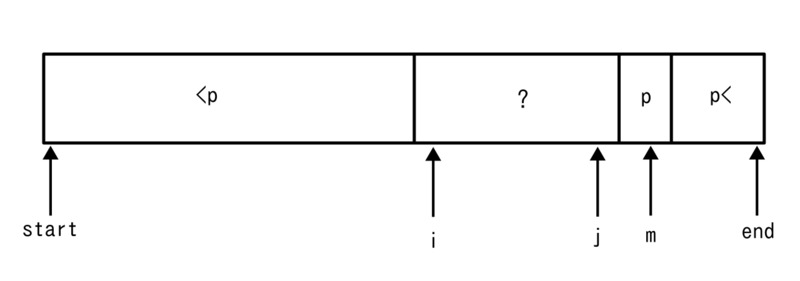
のようになり、i<=mかつm<=jの不変の表明が破られます。これによって、プログラムの正常な動作が保証されなくなります。
どのように修正するべきか
該当部分である箇所
|
1 2 3 4 5 6 7 |
if(i==m){ m = j; } else if(j==m){ m = i; } i = i+1; j = j-1; |
が不変の表明を守るためにはピボットがスワップしたときに配列が整列済みとならないようにiもしくはjの位置を動かさないようにすればいいでしょう。例えば
|
1 2 3 4 5 6 7 8 9 10 11 |
if(i==m){ m = j; i = i+1; continue; } else if(j==m){ m = i; j = j-1; continue; } i = i+1; j = j-1; |
にすることが考えられます。continue文が気になるのならば、
|
1 2 3 4 5 6 7 8 9 10 |
if(i==m){ m = j; i = i+1; } else if(j==m){ m = i; j = j-1; } else { i = i+1; j = j-1; } |
のようにするのも良いと思います。
個人的にもう一つ、気になる点があります。以下のコードの
|
1 2 3 4 5 6 |
if(start < i-1){ quicksort(a, start, m-1); } if(end > j+1){ quicksort(a, m+1, end); } |
if文の条件文が少し気になります。これはピボットから左右の配列に組分けできたときに再帰的にその配列に対してクイックソートを行う部分です。この左右の配列が存在するかどうかの判定がiやjが2つ以上動いたときにこの条件が通ります。これでも大丈夫ですが、せっかくmというピボット位置を作ったので、
|
1 2 3 4 5 6 |
if(start < m-1){ quicksort3(a, start, m-1); } if(end > m+1){ quicksort3(a, m+1, end); } |
みたいにするとmを抜いた、左の配列(a[m]以下の配列)と右の配列(a[m]以上の配列)を再帰的にクイックソートするという意味合いとして読み取りやすいかなと思いました。
最終的なコードと感想
最終的なクイックソートの関数は
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
function quicksort_fixed(a, start, end){ m = parseInt((start+end)/2); i = start; j = end; while(i<j){ while(a[i] < a[m]){ i = i+1; } while(a[j] > a[m]){ j = j-1; } if(i>=j){ break; } temp = a[i]; a[i] = a[j]; a[j] = temp; if(i==m){ m = j; i=i+1; } else if(j==m) { m = i; j=j-1; } else { i = i+1; j = j-1; } } if(start < m-1){ quicksort_fixed(a, start, m-1); } if(end > m+1){ quicksort_fixed(a, m+1, end); } } |
のように修正出来ました。この関数でさっきの上のような配列などもソートできるようになりました。
感想として、このクイックソートが高校の情報1のクイックソートの例としてふさわしいかどうかを考えると少々配列の部分分けに手間取っている感じがしてややこしくしている感じがあるので、分かりやすさの面としても紙面の都合としても少し良くない感じはあります。
python版の正誤表で直されたクイックソートではそもそもピボットの位置なんて概念はなく、iとjだけで再帰的に処理すべき部分配列を表しているので良い修正がされていると思いました。
今回は表明を使って、たまたまどのようなバグであるかが分かった(そういうデバッグの意味では良い例だった?)のでなんとなく記事にしてみました。私自身もアルゴリズムはあまり得意ではないので、クイックソートの良い勉強になりました。というわけで、これからも良くテストされた標準ライブラリのソート関数を使って生きていきたいと思いました。自分では実装したくない><
出典:高等学校情報科「情報Ⅰ」教員研修用教材:文部科学省 (2024.02.27 閲覧)
参考文献:「珠玉のプログラミング 本質を見抜いたアルゴリズムとデータ構造」(Jon Bentley著, 小林健一郎訳, 2014, 丸善出版, 原著「Programming Pearls Second Edition」)
